| It was with great
excitement that I learned that L. M. Milne-Thompson had written
a second book on fluid flow. This one was called “Theoretical
Aerodynamics”, a mate for “Theoretical Hydrodynamics”.
So it was off to “Mainly Books” again, to order
my copy over the internet. Here are some quotes from it.
“The science of aerodynamics is concerned with the
motion of air and of bodies moving through air”. Yup.
“Thus the effect of compressibility on a given profile
is to increase the lift in the ratio of 1:ß” [Beta
is the expression ß^2 = 1 – Mo^2), where Mo is
the Mach number in the undisturbed flow]. So far so good.
“Should places occur on the aerofoil where the critical
speed is attained or passed, shock waves may develop and part
of the regime may become supersonic. The investigation of
this mixed state is not yet on a satisfactory basis”
Yikes, I’ve done my dough! That regime is exactly the
one concerning propeller tips, the transonic region! Maybe
I was expecting too much of a book first published in 1948.
Still, compressible flow and supersonic flow are covered,
so I guess the $41 was well spent. So now I have to fall back
on Abbott and Von Doenhoff’s “Theory of Wing Sections”,
1949, and Ray Whitford’s “Design for Air Combat”,
1987: especially the latter.
What we are going to do now is look at 2 airfoil sections
operating in the transonic free-stream region, 0.7 < M
<1.0. That is where propeller tips are operating in F3D
and F2A, so any nasties hidden there we need to know about.

The question is: how do these airfoils in Figure 1 above
behave in the transonic region which exists at our propeller
tips? Maybe they are good, maybe bad, or maybe they may show
us a direction to go for propeller tip aerofoil design. Well.
We have some lift data for these sections as a function of
Mach number. Here they are in Figure 2.

The vertical axis represents lift. For the more pedantic,
the symbol (Cl) stands for lift coefficient, but it still
means lift. The horizontal axis is Mach number. Mach 1 is
the speed of sound, about 340 m/s.
We don’t need to look too closely to see that in the
region 0.7 < M < 1.0 things are bit of a mess. For the
NACA 0010-34 section, the lift increases steadily (as you
would expect from the effect of compressibility) up to about
Mach 0.75, but then it crashes down to less then its low speed
value. At least it is still making some lift!
But look at poor old NACA 2312! The lift crashes down below
zero! Hells Bells, it’s pushing backwards: it would
work better in the transonic region if the prop were put on
backwards!
Now NACA 0010-34, with its sharpish nose entry and zero camber
seems to be telling us not to use a blunt cambered section
like NACA 2312. Make a mental note of that, folks. Like, Note
1.
Well, lift is one factor, but so is drag. We had better see
how these sections go for drag in the transonic region. Here
they are in Figure 3.
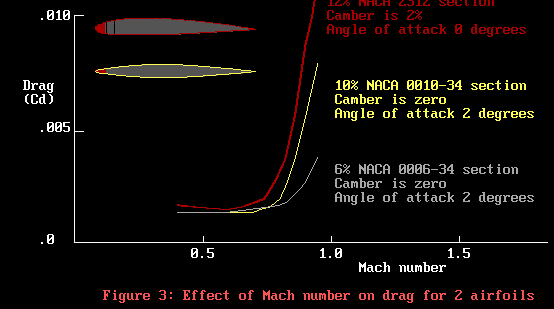
The vertical axis is drag. We don’t like drag, the engine
has to waste power overcoming drag when we really want it
to use that power to make thrust.
Well, there we are in trouble again with the transonic region.
Poor old NACA 2312 is rocketing up: even NACA 0010-34 is in
strife. Just for fun, I’ve added the data for NACA 0006-34.
Hmm, the drag of that thinner section is much lower. So it
wasn’t the camber of NACA 2312 that is the bother, as
both NACA 0010-34 and NACA 0006-34 have zero camber!
Maybe we can make this observation. All we have really done
to improve both the lift and drag in the transonic region
is to flatten out the curvature of the sections.
Now we have seen the problem, it is time to move on to some
more observations. But first, be aware that this could get
a little taxing on the grey matter. It certainly is on mine.
And not just mine. When I went to pick up my copy of Theoretical
Aerodynamics, she of the cash box went to pick it up off the
desk but could not find it. I suggested to my horror that
someone may have stolen it! She fixed me with the firm myopic
gaze of the career librarian and uttered “nobody would
steal THAT book!” I guess she must have had a peek at
the contents!
Right, now to hit you with the full carcase, in figure 4.
There is really too much info in this figure to absorb in
one sitting, so I will dissect it into smaller pieces as we
go along. That is, if you still have the stomach for all this!

OK, there is too much here. We’ll strip out some of
it to make Figure 4A below

Right, let’s start with the yellow bits.
The vertical axis (ordinate) is labelled P/Po. The P stands
for pressure. Po is the pressure at the stagnation point.
Since the stagnation point lies at the point where the flow
splits at the leading edge to flow over the upper and lower
surfaces, it is common to both surfaces. It is also the highest
pressure felt by the airfoil. The free-stream velocity of
Mach 0.75 determines the magnitude of the Po.
Thus P/Po is the ratio of the pressure at some point on the
airfoil surface to the stagnation pressure. As the stagnation
pressure is the highest, this ratio will be less than unity.
Hence the scale is marked, upside down, as .8, .6, .4, .2
down to zero. Zero is pretty low, I guess that would amount
to a vacuum!
The green line represents the happenings on the upper surface.
At the start point where x / c = 0, P / Po is unity, which
is fair enough since it’s the stagnation point, so P
= Po! Moving up the green line, P is falling as the air accelerates
to high subsonic speed. In this case, the local speed actually
gets to exceed Mach 1 slightly, but this speed is not enough
to generate a shock wave.
Note that in moving from the stagnation point to around the
leading edge, the air has gained a velocity comparable to
the speed of sound. Man, that is really accelerating.
Like Captain Kirk says of Warp 5, you can’t do that
on the freeway! We are right into the zone of compressibility
here, and the lift coefficient has climbed from the initial
value at low speed of about .16 to something like .34. Lots
of suction in that area, as is made visible in green on the
photos in my earlier treatises on transonic airfoils.
As x/c increases….? What is that x/c label on the lower
axis (abcissa)? Well that is standard nomenclature for the
distance along the airfoil. The letter c stands for the chord.
A representative value for an F3D prop might be 13mm. Looking
again at Figure 4A, you will see the airfoil drawn at the
top. The drawing is to scale. The leading edge is at x/c =
0, and the trailing edge at x/c = 1. A possible value for
x might be 6mm. Then x/c = 6/13 = 0.46. Naturally, x cannot
be greater than c.
But we digress. As x/c increases, the local velocity falls
below Mach 1 and the air expands, with an associated increase
in pressure, so P/Po increases. Near the trailing edge, the
flow tends to break away and the pressure increases further.
OK, that finishes looking at Figure 4A. Now we can add the
lower surface pressure in Figure 4B.

We have added the lower surface in dark blue. Nothing else
has changed.
Because the airfoil is operating at an angle of attack of
2 degrees, something magical happens. The speed of the air
over the lower surface is less than that over the upper surface,
so the pressure drop is less. The fact that the lower surface
is at a higher pressure than the upper surface means that
there is a net lifting force acting on the airfoil.
As x/c exceeds about 0.1, the local velocity increases slowly
as the air follows the airfoil curvature and the pressure
falls slowly. At about x/c = 0.7, the air tries to follow
the upward curve of the airfoil undersurface, expand and the
pressure rises as the air approaches the trailing edge.
Nearly there. Consider Figure 4C below. Oops, I think it’s
the same as Figure 4!
Yup, it is. But compared to Figures 4A and 4B, we have added
another axis! Neat trick, what? The right hand ordinate is
labelled “Local Mach#”

Well, is this a bit weird? Yup, sure is. First off, the labels
0.4, 0.6, 0.8 etc are not equally spaced. The scale is non-linear,
whereas the scale for P/Po is linear.
The fact that we can plot P/Po and Local Mach# both on vertical
axes has a meaning. That meaning is that the values of P/Po
and Local Mach# depend on each other in a fixed way. Ie, P/Po
can be calculated if we know Local Mach#, and vice versa.
So what is Local Mach#? Well, remember how the air has speeded
up going from the stagnation point and wending its way over
the airfoil surfaces? We have that for any value of x/c, we
can read off the value of the local air-speed by going up
to the chosen surface, then across to the right hand axis.
Here is an example. Choose x/c = .5 (mid-chord). Move up
to the green line, which is the upper surface. Then the speed
of flow at that point is about Mach 0.92. Neat, huh?
Since Mach 1 is about 340 m/s, the speed of the air is then
340*.92 = 313 m/s. Make no mistake, this is fast. A typical
F3D model does about 80 m/s.
Now for the main point. The Mach# and the pressure of the
airflow are not accidentally related. The high speed airflow
over the surface CAUSES the change in pressure at x/c. This
is how airfoils work: if we want lift, or for propellers,
thrust, then we have to blow air over them. This causes a
drop in pressure. If the pressure drop is greater over the
upper surface than over the lower surface, then well and good,
we have lift.
In the unfortunate case of NACA 2312 at Mach .85, the opposite
is true: we have reverse thrust! No good, that airfoil is
definitely the wrong shape!
So what is the right shape? Well. We are not yet ready to
answer that, as our example for a free-stream velocity is
only Mach 0.75. But our prop tips go up to Mach .95: there
is still plenty to go wrong, believe me!
All very nice, Mach 0.75 is not really what you would call
transonic flow. To get that, we will have to speed up the
air incident on the airfoil. Lets jump to a free-stream speed
of Mach 0.81. Now we should see some fun and games! (read
TROUBLE!)

Check out the airfoil sketch. At x/c about 0.75 I have added
a shock wave in red. What is that doing there? Well, directly
below it. In green we can see that the local velocity has
dropped below Mach 1. When this transition occurs, in quite
a marvellous fashion there is a near instantaneous drop in
speed, increase in pressure and rise in temperature. The transition
point is marked by the position of the shock wave.
In figure 5, the flow speed in front of the shock is about
Mach 1.2, while behind the shock, it has dropped suddenly
to about Mach 0.9. How can that be? Where have all the air
molecules gone that entered the shock wave? Well they are
still there, but jammed up against each other: that is to
say, their pressure and density have both increased, compared
to in front of the shock.
Nothing much has happened on the lower surface. The local
velocity has not yet exceeded Mach 1, so no shock has formed.
We still have lift, but what about the drag?
The problem with shock waves is that they interrupt the nice
smooth flow over the surface. We need that smooth flow to
make the low pressure. Behind the shock, the pressure has
increased; not what we want for making lift on the suction
(upper) side of the airfoil. Even worse, the shock disrupts
the smooth flow close to the airfoil surface. This air very
close to the surface tends to stick to the surface: it has
a special name. It is the “boundary layer”. The
pressures we need to make lift have to get thru the boundary
layer to push on the airfoil surfaces. If the boundary layer
thickens, then a deep wake is produced which increases the
drag.
Regrettably, that is just the effect the shock wave has on
the boundary layer. The stronger the shock, the worse the
wake drag. So shock waves are doubly bad: loss of suction
and increase in drag.
Things can get worse. Let’s try a free-stream velocity
of Mach 0.89.

Focus first on the airfoil sketch. The upper surface shock
has moved back, and we now have a lower surface shock to add
to our woes. Even worse, the pressure on the lower surface
behind x/c = 0.7 is less than that on the upper surface. We
now have suction on the lower surface, and reduced pressure
on the upper surface. Not what you want for lift. Add this
to the drag caused by the 2 shocks affecting the wake flow,
and we would gladly see the last of these shocks.
Now all this drama is happening about 10mm in from our F3D
prop tips. We are deep into the transonic flow problems caused
by shock waves. Lift is poor, drag is high: if shock waves
were teeth, you’d have them extracted!
Now lets go for a full set of dentures. Mach 0.98.

Both shocks are now at the trailing edge. Drag has skyrocketed
due to the wake turbulence. Incredibly, lift has improved,
as the upper surface pressure line no longer crosses the lower
surface pressure line. The flow is supersonic everywhere,
except at the leading edge. I think the best thing you could
say is that the shocks have moved off the section nearly altogether.
At this point you may be asking ( again) why the lower surface
pressure curve is below the upper surface pressure curve on
the diagram. It is a magical fact that flow over the lower
surface of an airfoil that is operating at an angle of incidence
is slower than that over the upper surface. There is a phenomenon
called “circulation” responsible for this behaviour.
I am not. I just want to get a better propeller airfoil.
OK, I have said most of what I wanted. You can see how shock
waves are a pest. In Part 2 I mentioned supercritical sections,
for use in the transonic region.
To reiterate, the upper surface shock can be reduced by reducing
the upper surface curvature. That is, flattening it out. What
is more, the lower surface can be modified to reduce the lower
surface shock and increase the pressure on that surface.
This trick is achieved by bending the trailing edge down
a bit, to form a shape known as a “cusp”. This
cusp reduces the lower surface flow speed, thereby weakening
the shock and increasing lower surface pressure at the trailing
edge. If the cusp is large enough, the lower surface shock
actually can move forward from the trailing edge and shrink
until it disappears altogether.
That’s about it: the shock has been laid bare. There
are some neat calculations one can do for the behaviour of
shocks in parallel ducts. These are illustrative, maybe the
subject for Part 4. Meantime, I shall return to the fluid
dynamics problem of determining the inflow field to a propeller,
as influenced by the spinner and cowling.
Watch this space. Cheers.
References:
1. “Theory of Wing Sections”. Ira H. Abbott and
Albert E. von Doenhoff, 1959. SBN 486-60586-8. Dover Publications,
Inc, New York.
2. “Design for Air Combat”. Ray Whitford, 1987.
Jane’s.
|