| You've backed up for still more? I assume you have read
Parts 1,
2 and
3 as otherwise this Part
4 will be incomprehensible. If not, here is a brief reprise.
So our fluid dynamics problem is to represent the flow of
air over a cliff or hill, on some sort of diagram. This diagram
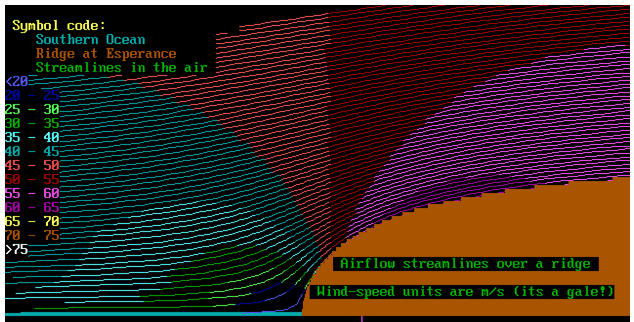
will have lines on it, like contours, called "streamlines":
also, it will have a picture of a cliff or hill. We have a hill.
It looks out over the Southern Ocean, so wind-farms and slope
soaring are “de rigeur”.
So now we get a definition. The path the wind follows is a
"streamline". The same air remains in the streamline, but it can
go faster: its pressure and density can change, but it is still
the same streamline, with the same air.
Now it would be interesting to know the pressure
distribution as well, but how do we get it?
Fortunately Edward R. C. Miles, a research mathematician at The
Johns Hopkins University at Baltimore, USA, 1950, felt the need
to publish a book called “Supersonic Aerodynamics”. On page 13
of this book he has the Saint-Venant and Wantzel equation, which
is a version of the Bernoulli Equation adapted to adiabatic
flow. The beauty of this equation is that it relates pressure to
velocity directly: ie, knowing velocity, we can easily calculate
the pressure.
Don’t worry about this maths too much, I have entered the
equation into my computer and we can see the result below.

For the non-mathematically minded, here is a plot of the
streamlines. The colours indicate the pressure bands present in
the streamlines. Look carefully and you will find that the
pressure at the bottom of the cliff is right up. In fact, at the
bottom of the cliff the wind has stopped. This is called the
"stagnation point".
What we find is that when the wind-speed is high, the air
pressure is low.
OK. Now we can move on. Hands up if your understand any of this.
Well, that was risky, because here are the trick questions.
- Why does the wind blow over the ridge? Why does it not
just give up and stop?
- Some of the air actually speeds up. This means that the
kinetic energy of the parcel of air in that region has
increased. Where did that energy come from?
Hey, now you wish you hadn’t put your hand up! Never
volunteer, never stand out from the mob, and never try to
outsmart Supercool!
In my youth, my first car was a Ford Prefect, 1950 model. At
only 10 years, it was an old bomb. But I got it for $100, did
30000 miles in it in 4 years, and figured that was a good deal.
The engine was side valve, which meant that the inlet and
exhaust valves were beside the cylinders, operated by pushrods
from down near the crankshaft: not overhead valves like today.
The exhaust valves used to burn out, which meant most times only
about 2 cylinders were working, which left about 5 HP for my
motoring!
I recall returning one evening from the Central Western C/L
champs in Orange. This meant climbing up over the Blue Mountains
before coasting down the other side in neutral to get to Sydney.
The old girl chugged along at about 10 MPH, slowly but
inevitably getting to the top. Do you remember, prof?
With my headlights on, I felt like the head of a comet, with a
long tail of other headlights winding away into the depths
behind me. I guess I won’t know that thrill again in this
lifetime, but the way my 1994 Toyota Camry keeps breaking down,
I might yet, but this time it will be the wretched thing
burning, by my hand.
Now here is my point. At least the old Ford had a source of
energy to get it up over the mountain: but I don’t see that the
wind is so supplied, so how does it get over the mountain?
Surely the old Ford would stop as soon as I turned off the
engine: but the wind seems to make it over anyway. Weird.
Well, lets be clear about this. Air is weird. Everything about
air is weird. It never does what you want, and it holds its
secrets very close.
The best we can do is invent a sort of simplified air, hoping
that perhaps SA (Simplified Air) will behave a bit like real
air.
So here we go. We will assign these properties to SA
- SA is incompressible. This is rubbish, because real air
compresses very easily: but even so, for air flowing fairly
slowly, say up to 100 MPH, we will not be too far wrong.
Don’t believe me, just suspend disbelief!
- SA is irrotational. Good grief, what does the mean?
Well, it has no eddies, and just flows smoothly. That’s fair
enough.
- SA is warm. That is, the molecules in the air are all
racing around like Emu chicks frightened by a Dingo. We will
measure this property in terms of temperature.
Now consider a parcel of air climbing up over the ridge. We
have seen that it speeds up and the pressure drops.
Well, it’s nice that the pressure drops, at least its flowing
from a region of higher pressure to one of lower pressure. That
figures. But how can its energy increase when it speeds up?
Surely the energy is not coming from the ridge, as the ridge is
inert. And the energy can’t come from behind, as there is no
mode for its transmission forward.
Maybe its pressure energy (whatever that is). After all, the SA
starts with high pressure and this falls. Maybe the pressure in
the air means that it is compressed, like a spring, and, as it
expands, it speeds up the air.
Well no, we already decided that SA is incompressible. Ok, so it
sure does have pressure, but being incompressible, it can
neither compress nor expand. That’s what the words mean. Can’t
be that.
So, all that is left to us as a property of SA is temperature.
All those molecules dashing about suggest that there is heat
energy available in SA.
So this can all happen if heat energy converts into kinetic
energy!
Well, that must mean that where the air speeds up, the
temperature must fall. So it really is cold up there on the
ridge! And it is warm down there with Horace, as the air is
nearly stopped!
Final words of wisdom. Air really is weird. When we need to
discuss air in terms of temperature and pressure, we have
entered a new world: the study of this new world is called
thermodynamics.
|